Dubbi sulle misure minima e massima
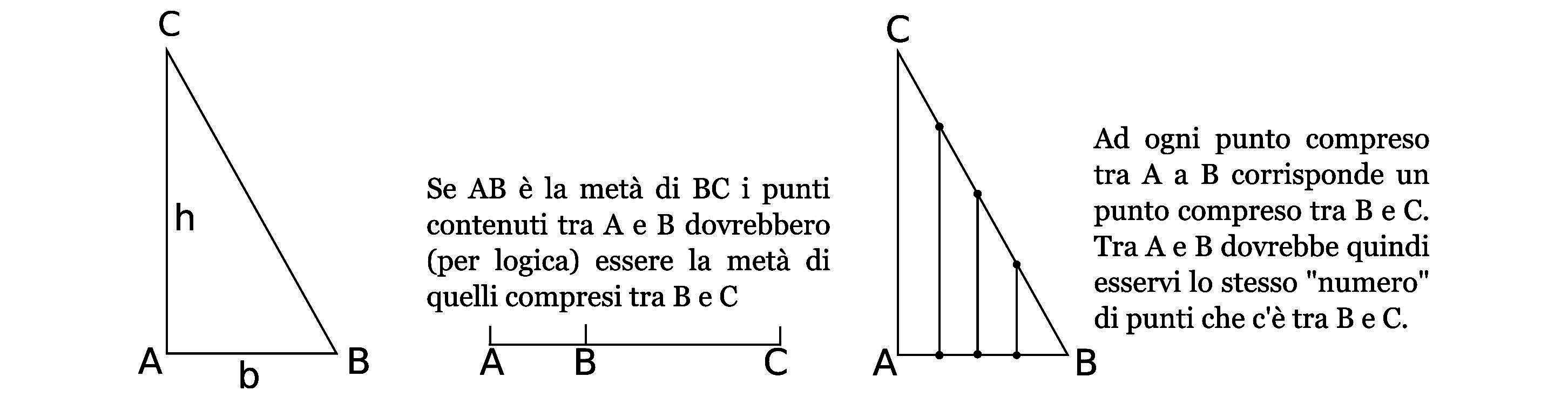
Fig. 1 – Tanti punti in AB quanti in BC?
Come abbiamo appena visto, teorie e ipotesi si basano spesso su assiomi, verità evidenti che non hanno bisogno di essere dimostrate.
Alcuni assiomi, però, non sono del tutto in armonia con i numeri, l’aritmetica, l’algebra e l’analisi matematica. Propongono infatti una logica completamente diversa, indipendente sia dallo spazio geometrico reale sia dallo spazio tempo, illusorio in quanto partorito dalla mente.
Ad esempio, ricordando l’assioma delle parallele di Euclide, si potrebbe arrivare ad affermare che due segmenti di diversa lunghezza contengono lo stesso “numero” di punti(1). Infatti, per la matematica, tra due punti qualunque di un segmento ne esistono sempre infiniti (Fig. 1).
Se la distanza tra A e B, indicata con b, diviene infinitesimale(2), AB contiene ancora la medesima quantità di punti di BC (Fig. 2)?

Fig. 2 – Se b diviene infinitesimale, può AB contenere ancora lo stesso numero di punti di BC?
Se poi il punto C tendesse all’infinito, la retta h – anch’essa tendente all’infinito – avrebbe sempre gli stessi punti di AB, divenuto infinitesimo? In questo caso la retta infinita BC, cioè AC (h), sarebbe uguale all’infinitesimo in AB.
In realtà non credo che l’assioma delle parallele di Euclide sia impossibile, ma dovremmo immaginare, nell’infinitesimo, un punto contenente innumerevoli dimensioni(3) che permettano il collegamento in parallelo con i punti in qualsiasi dimensione. Sembra un paradosso irrisolvibile. Il punto matematico, infatti, è un’astrazione posizionata nello spazio e le rette sono un’infinita serie di punti; allora ogni linea è un’infinita serie di “astratti”, cioè niente, zero.
∞ moltiplicato zero è quantità di…?(4)
Credo vada riconsiderato lo Zero, cioè il Nulla, e quindi l’infinito. In un’unica definizione: il “Bordo Nulla”.
I paradossi dell’infinito sono stati aggirati (alcuni matematici dicono “risolti”, ma sono troppo ignorante in materia per capire perché venga usato questo termine) utilizzando la matematica transfinita(5). Ritengo che sia uno dei soliti espedienti con cui si vuole mantenere la scienza in una “torre d’avorio”. O meglio, spacciare un banale osso per un prezioso avorio che dovrebbe rimanere nelle zanne dell’elefante. Cioè pura e semplice Natura, Realtà.
La questione andrebbe rivista e finalmente dipanata, se possibile, in base al vero valore della parola “risolvere” e non attraverso invenzioni matematiche che a volte, pur aggirandosi nei dintorni, non sono nemmeno lontanamente coerenti con la realtà. Infatti, tra un valore matematico e un altro, anche con molti zeri dopo la virgola, c’è sempre una distanza infinita.
La matematica è astratta, allora forse la soluzione è nella Realtà dello 0 (zero) e nell’infinito. O meglio nella quantità di un “certo” zero risultante dalla moltiplicazione ∞ ∙ 0, che è qualcosa: noi!
Resta il “nostro” ∞ (infinito) contenitore, l’Artefice della creazione. Noi, affacciati alla finestra, senza confini, ne percepiamo il Bordo Nulla.
Si può teorizzare che il Nulla Assoluto, a cui l’universo(6) si rivolge, si affacci a Infiniti universi semplicemente affacciati a noi, coscienza dell’universo. Noi, infinitesimali, siamo affacciati a questo Bordo attraverso quel Nulla (Assoluto, Dio, contenitore di infiniti universi, ecc.) per il quale “Coscienza” è il Termine Reale di Chi la matematica “È”: l’Assoluto, che è la Creazione di ciò che ha portato alla coscienza(7).
Tornando alla geometria, ipotizziamo innumerevoli circonferenze concentriche (non infinite). Tutte le rette che partono dal centro comune mettono in corrispondenza ogni punto delle circonferenze “minori” con ciascun punto di quelle maggiori, esaurendoli completamente (Fig. 3).
Questo, tuttavia, non è possibile, a causa della differente lunghezza di ogni circonferenza (Fig. 4).
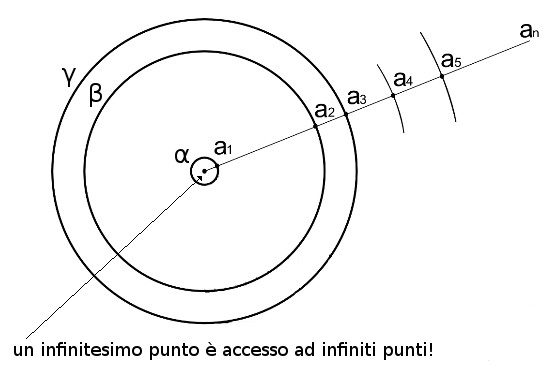
Fig. 3 – Considerando una serie di circonferenze concentriche, si può ipotizzare che, per ogni punto di ciascuna circonferenza, esista un punto corrispondente in tutte le altre. Quindi, ad esempio, per il punto (a1) della circonferenza α esiste un punto corrispondente (a2) nella circonferenza β, un punto (a3) nella circonferenza γ e così via.
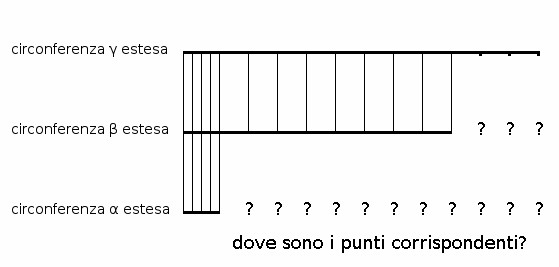
Fig. 4 – Linearizzando le circonferenze α, β e γ della figura precedente, risulta evidente che, a causa della diversa lunghezza, non è possibile che per ogni punto di ciascuna circonferenza ci sia un punto corrispondente in ognuna delle altre.
Come evidenziato da Giovanni Duns Scoto: “è impossibile che due cerchi ineguali si compongano di parti uguali in numero e grandezza. I punti sono uguali per definizione, e siccome ve ne sarebbero nella circonferenza del piccolo cerchio tanti quanti in quella del grande, il più piccolo sarà uguale al più grande e la parte al tutto, il che è impossibile.”(8)
Si arriva così a un paradosso dello stesso tipo di quello generato dall’assioma delle parallele di Euclide e dall’ipotesi degli infiniti punti di un segmento: avremmo, infatti, anche in questo caso, gli stessi punti nella circonferenza infinitesima e in quella infinita.
Tutto ciò dimostra che il punto matematico-geometrico è pura fantasia, illusione… come si può formulare una teoria fisica partendo da un simile presupposto? Penso sia necessario proporre nuove basi ipotetiche (basi certe sarà difficile) riallacciandoci alla fisica sub-nucleare.
Concepiamo un ipotetico quark(9): la dimensione minima (1Qm). Se l’energia diviene massa-materia, vuol dire che a un certo punto si passa da una possibile misurazione non spaziale a una spaziale, a due o tre dimensioni.
Ridefiniamo quindi il concetto di punto fisico: unico al centro è un “quanto” di energia, o un quark. Oppure…? Chi può dirlo… Lo stesso Einstein ripeteva che non ci si può definire scienziati se non si ammette l’insondabile mistero.
Detto ciò, possiamo iniziare a considerare circonferenze più reali in una Geometria Universale, ognuna fatta non di “infiniti” punti teorici, ma di una reale quantità di quark, in fila e in numero uguale. Sempre che esistano, come si teorizza.
Possiamo ipotizzare un’unificazione a tempo zero dei “partecipi” alla materia, in quanto presenti e assenti sul bordo dell’esistere, anche come forma?
Per rispondere a questa domanda dobbiamo cominciare a teorizzare una nuova matematica applicata alla fisica, dove si tralasciano, per ora, i concetti di infinitesimo e infinito, e si sostituisce al tempo il Bordo Nulla: un Recipiente Infinito di Energia, presente in ogni punto spaziale dove sia visibile e/o concepibile un evento energetico di particelle.
Per fare un esempio (anche se gli esempi non sono mai realmente calzanti) pensate a una pentola. Quando l’acqua raggiunge l’ebollizione, ce ne accorgiamo osservando l’effetto sulla superficie del recipiente: bolle, spruzzi, vapore, energia termica. Ebbene, così funziona anche il nostro universo.
(1) ^ Assioma delle parallele: “in un piano, per un punto esterno a una retta passa una e una sola parallela a quella data”. L’assioma delle parallele consente di mettere in corrispondenza biunivoca i punti del segmento AB con quelli del segmento BC (Fig 1.1). All’inizio del XIX secolo i risultati delle ricerche di Gauss, Bolyai e Lobacevsky segnarono una profonda crisi della geometria, in quanto mostrarono che il quinto postulato di Euclide (equivalente all’assioma delle parallele) era indipendente dai precedenti quattro e che pertanto era possibile costruire nuove geometrie, dette non euclidee, nelle quali il quinto postulato non era valido.
(2) ^ Gli infinitesimi sono entità numeriche infinitamente piccole introdotte da Gottfried Leibniz, che ne fece il fondamento del calcolo infinitesimale. Sono minori di qualsiasi numero reale positivo eppure ancora maggiori di zero. Nella loro definizione oscillano tra una concezione attuale (sono enti matematici effettivi) e una potenziale (esprimono semplicemente un avvicinamento infinito allo zero).
(3) ^ Innumerevoli dimensioni, in quanto “infinite” nella Realtà non è concepibile.
(4) ^ In matematica moltiplicando ∞ per 0 si ottiene un prodotto indeterminato.
(5) ^ I numeri naturali non sono tanti quanti i punti della Retta Reale, ma di meno. I numeri reali sono tanti quanti i punti della suddetta Retta. Georg Cantor, partendo da ciò, dimostrò che non tutti gli infiniti sono uguali, ma esistono diversi insiemi infiniti e li classificò in base alla quantità dei loro elementi. All’epoca la questione era scottante, in quanto l’infinito appariva essere argomento più da teologi che da matematici. Pertanto Cantor, che si occupava anche di teologia, distinse due infiniti: Infinito Assoluto (proprio solo di Dio e non umanamente percepibile o individuabile attraverso la scienza) e infinito matematico (denominato transfinito per evidenziarne la differenza dal primo).
(6) ^ Limitato, non infinito per quanto riguarda materia e/o energia.
(7) ^ Quindi ricostruire, replicare la “creazione” di ciò che ha portato alla coscienza.
(8) ^ Étienne Gilson. Giovanni Duns Scoto. Jaca Book, Milano, 2007, pag. 431.
(9) ^ Non credendo nelle stringhe parleremo di quark. Non essendo stata né accertata né spiegata, quella delle stringhe non è una teoria; a quanto ne sappiamo la loro esistenza rimane un’ipotesi. Su cosa si basa questo assioma?